Circuits
When resistances are connected in series, the sum of the resistances in the
circuit will equal the equivalent resistance(the resistance that would be there
if there were only one resistor) R_eq = R_1 + R_2 +.. etc. The sum of the voltage
V1+V2+V3.. equals the total voltage V. Since this is true, then V = IR_eq. When
in parallel, the reciprrocal of the total resistance equals the sum of the reciprocols
of the individual resistances.. 1/R_eq = 1/R_1 + 1/R_2, etc. I, the total current
is the sum of the partial currents. I = I_1 + I_2 + I_3.. etc. I = V/R_eq. ACCORDING
TO RETROPUNK, if you have two parallel resistors, R1, R2, then the equivalent
resistance is R1*R2/(R1+R2)
Finding net capacitance is just the opposite. When in parallel, the sum of
the individual capacitances equals the net capacitance. When in series, 1/net
capacitance would equal 1/C1 + 1/C2 +1/C3.. and so on.
Terminal voltage from point a to point b = electromotiveforce - Ir. the internal
resistance is r, I is current, electromotive force is the potential difference
between the terminals of a source like a battery when no current flows to an
external circuit, or in other words when no other device is connected.
The sum of the potential difference around a closed circuit is 0. ( LOOP RULE,
Kirchoff ) The sum of the current entering a junction and the current leaving
a junction is equal to 0. ( JUNCTION RULE, Kirchoff )
| The cube made of resistors.. Sorry, no picture! |
Having a cube of wires, each wire acting as a R-ohm resistor, and the cube is connected to the circuit through it's diagonals, that is, two opposite corners. Find the equivalent resistance.
This problem seems rather complex, but by spending some time analyzing the situation, you can break down this cube of resistors into a simple circuit. Starting at one corner, the current will split into three parallel resistors. Every wire that has the same potential can be "connected." This is because no current will flow through the connection. We then have the first part of the cube, three resistors in parallel. The next step is to bridge the mass of resistors to get back to the other corner via 3 more parallel resistors ( symmetry of the cube ). There are six resistors left in the middle. They are actually in parallel with each other if you draw out the cube as a flattened cube ( try it! ).
Putting it all together, we arrive at (3(1/R))^-1 + (6(1/R))^-1 + (3(1/R))^-1 => (5/6)*R
|
Wheatstone Bridge
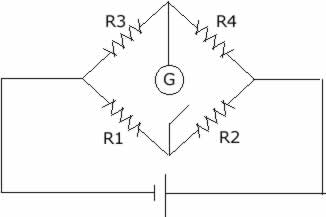
|
This is a circuit used to make precise measurements of resistance.
Generally speaking R4 is the unknown resistance. Try deriving the following
formula! "R4*R1 = R2*R3"
Voltage through arm 2 is equal to voltage to arm 4., voltage through
arm 1 is equal to voltage through arm 3. The voltage through the galvanometer
is 0, no current through the galvanometer either. From this we can deduce
that I1 = I2, and I3 = I4. V2 = I2R2. V4 = I4R4. Since V4 = V2, then I2R2
= I4R4 is true. The total voltage equals V2 + V1 and also equals V3 +
V4. Since V2 = V4, then V4 + V1 = V3 + V4, V1 = V3.
V1 = I1R1, V3 = I3R3. From above, I1 = I2, I3 = I4.
V1 = V3.
I1R1 = I3R3
I2R1 = I4R3, from above I2R2 = I4R4, divide the two.
R1/R2 = R3/R4.
R4R1/R2 = R3.
R4 = R2R3/R1.
|
The T-Circuit
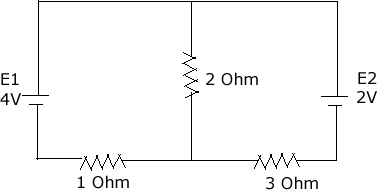 |
This is the T-Circuit.
Try to solve for the current in each branch! BECAUSE PHYSICS IS FUN AND
EVERYONE LOVES PHYSICS!!@%
I2 = I1 + I3 JUNCTION
E1 = I2R2 + I1R1 LOOP
E1 + I3R3 = E2 + I1R1 LOOP
Since I2 = I1+I3, then eq 2 can be rewritten as E1 = I1R2 + I3R2 + I1R1.
(Thanks for correction Jaia)
Also, retropunk's suggested node voltage method: (V(2ohm) - E1) + V(2ohm)/2 + (V(2ohm) - E2)/3 =0
|
RC Circuits
Resistor capacitor circuits are a special kind of circuit. Here we begin
to dive back into charges and the such.
tau = time constant = RC, measures how quickly a capacitor charges.
half-life(the time it takes to charge the capacitor to half full)= tau * ln
2
Capacitor Charging formulas.
V = emf(1-e^-t/RC)
q = q_0(1-e^-t/RC) , q is charge, q_0 is max charge.
Capacitor Discharging formula
V = V_0(e^-t/RC), V_0 being the initial voltage.
Problem 1
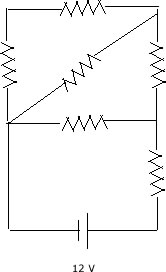 |
In the diagram to the left, each of the resistors
have a resistance of 2 ohms. Find the equivalent resistance throughout
the circuit.
To tackle circuit problems, basically all you want to do is look where
you can start simplifying. For starters, the top left and top center resistances
can be added together to get 2R since they are in series. Next you can
simplify again by taking the recipricol of that and adding the recipricol
of R, the diagonal resistance. Next, it acts as in series with the resistor
in the top right. so add that. Here is what you should have so far.. (2R^-1
+ R^-1)^-1 +R. Next, is the middle horizontal resistor, which is in parallel
with what we have so far.. So we now have. (((2R^-1 + R^-1)^-1 +R)^-1
+ R^-1)^-1. And to finish it off, we add the resistor closest to the power
source as a series. (((2R^-1 + R^-1)^-1 +R)^-1 + R^-1)^-1 + R. Yeah..
it's a little messy but breaking it down will help. You can also redraw
the diagram as a circuit getting rid of the diagonal resistor.
So, just substitute 2 ohms in for R, and you will get 3.25 ohms. |
Problem 2
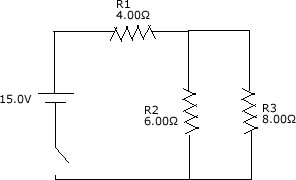 |
Find I1, I2, I3, V1, V2, V3 and the power loss
in R3.
Start off by finding the equivalent resistance, R1+ (R2^-1 +R3^-1)^-1
=> 7.4 ohms. Now, use the equation V_powersupply = I_total*R_eq. 15/7.4
= 2.027A. R1 will receive the full current since it isn't in parallel
with anything and has a series connection to the power supply. So, I1
= 2.027A. Solve for V1 by multiplying by R, 2.027*4.00 = 8.1V. Use the
loop rule now, V_powersupply - V1 = V2 = V3. So, 15.0V - 8.1 = 6.9V for
both V2 and V3. Now you can apply Ohm's law, and find the current to I2
is 1.15A, and I3 is 0.8625A.
The power loss in R3 is simply P = I^2R(or P = IV), so P = (0.8625^2)(8.00)
= 5.95W. |
Problem 3
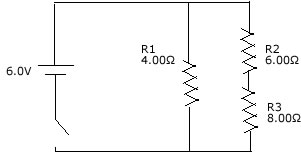 |
Find I1, I2, I3, V1, V2, V3 and the power loss
in R3.
Find the equivalent resistance of the circuit.. Should be (R1^-1 + (R2+R3)^-1)^-1.
This will equate 3 ohms. Now that you have the equivalent resistance,
V_powersupply = I_total*R_eq, 6.0V/3.0 ohms = 2.0 Amps for total current.
Use the loop rule to determine that V_powersupply = V1, so V1= 6.0V. Now
solve for I1, 6.0V/6.0 ohms= 1.0A. Since we found the current to this
branch of the junction, then the total minus this current must be the
current for the branch that R2 and R3 resides on. I_total - I1 = 1.0A.
Thus I2 and I3 are 1.0A since they are in series. Now, solve for V2 and
V3 by Ohm's law, giving 4V and 2V respectively. |
Problem 4
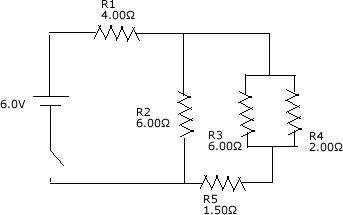 |
Find I1, I2, I3, I4, I5, V1, V2, V3, V4, V5
and the power loss in R.
Find the equivalent resistance of the circuit. R1 + (R2^-1 + ((R3^-1+R4^-1)^-1+R5)^-1
= 6 ohms. V_powersupply = I_total*R_eq, 6.0V/6.0 ohms = 1A for total current.
R1 receives the full current since it is in series, I1 = 1A. Solve for
V1 by Ohm's law; 4.0V. Use the loop rule to find V2 now, V_powersupply
- V1 = V2, 6.0-4.0 = 2.0V. Use Ohm's law again to find I2, which is 0.33A.
Now, find the current for the branch containing R3, R4 and R5. Since I2
is 0.33A, and the total current is 1.0A, the current entering that branch
must be the difference, 0.66A. Since R5 is in series with that current,
I5 = 0.66A, use V = IR to find V5 to be 1V. Since V5 is 1, then the loop
rule says V_powersupply - V1 - R5 = (V3+V4). 6 - 4 - 1 = 1V, so the voltage
is 1V for V3 and V4 because the voltage through parallel resistors is
equivalent. Now use Ohm's law again to solve for the currents. I3 = 0.1667A,
I4 = 0.5A |
Problem 5 (kudos paul)
A 2.8 kilo-ohm and 2.1 kilo-ohm resistor are connected in parallel this combination
is connected in series with a 1.8 kilo-ohm resistor. If each resistor is rated
at 1/2W, what is the maximum voltage that can be applied across the whole network?
Since this problem is querying for the max voltage, this means that the answer
will depend on the resistors. Each resistor having a rating of 1/2W means that
only 1/2W is allowed, or else it will blow up like an overcooked chicken (note:
not a bad thing to do!) HAha.. anyway. The equivalent resistance for just the
parallels would be ((2.8x10^3)^-1 + (2.1x10^3)^-1)^-1 => 1200 ohms. The total
equivalent resistance would be 3000 ohms. Let R1 be the 1800 ohm resistor, R2
the 2100 ohm resistor, R3 the 2800 ohm resistor.
For resistor 1, P = V^2/R. Although we know P and R, we need to find a way
to express the applied voltage. You know the current will split at the parallel
branch, and then the sum of the current here will equal the current running
to the 1.8 kilo-ohm resistor. Let's consider the 1.8 kilo-ohm resistor first.
If a current is running through the resistor, then voltage can be found via
V = IR. R is 1800ohm. If the equivalent resistance is 3000ohm, then the current
can also be expressed aby V_powersource = I*3000. As you can see, these are
in a ratio of sorts. 1800/3000 is used in expressing V_max. From P = V^2/R,
1/2W = (1800/3000V)^2/(1800) 1800 being the resistance of the resistor, solving
for V will result in 50V or -50V.
For resistor 2, P = V^2/R. Just like for resistor 1, we have generalized how
to approach this. Keeping in mind that the R divided by the equivalent resistance
will be the R that the current encounters when traveling to a parallel branch.
So, use the 1200ohm. 1/2W= (1200/3000V)^2/2100 => 81V or -81V.
For resistor 3, P = V^2/R, repeat.. 1/2W = (1200/3000V)^2/2800 => 93.54V
or -93.54V
Looks like 50V is the lowest voltage, so 50V is the maximum voltage that can
be applied across the whole network.
Problem 6
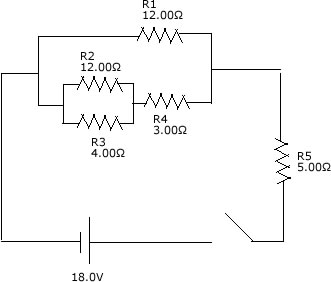 |
You know the deal.. Find I1, I2, I3, I4, I5,
V1, V2, V3, V4, V5 and the power loss in R3.
R_eq should be (((R2^-1+r3^-1)+R4)^-1+R1^-1)^-1 +R5, which equates to
9.00 ohms. Find I_total by V = IR, 18/9 = 2 amps. R5 is the only resistor
that will get the full current of 2 amps, so I5 = 2A, V5 = 10. Now that
we have found the potential difference for R5, we can find the potential
difference running through the parallel branch by the loop rule. V_source
- V5 = Par branch. 18V - 10V = 8V goes to the branch. Since R1 is not
in series with another circuit, it will get the full 8V, so V1 = 8V, I1
= 0.6667 amps. Use the junction rule to find the current running through
the lower branch containing R2 R3 and R4, I_total - I1 = current through
branch, 2 - 0.6667 = 1.333 amps. R4 is not in parallel so it will receive
that full 1.333 amps, I4 = 1.333 amps. V4 = 3.999V. Now we are left with
R2 and R3. By the loop rule, V1 - V4 = V2 = V3(since R2 and R3 are in
parallel they receive the same voltage). So, 8 - 3.999...= 4V. Now that
you have V2 and V3 equal to 4V, solve for I2 and I3, which are 0.333 amps
and 1 amp respectively.
To find the power loss in R3, use P=I^2R, which will give you 4W. |
Problem 7
An unknown length of platinum wire, 0.92 mm in diameter is placed as
the unknown resistance in a Wheatstone bridge(see top). R1 is 38 ohms, R2 is
46 ohms, Balanced is achieved when R3 is 3.48 ohms. How long is the platinum
wire?
Remember R = pL/A from the Electric Currents section? Well, that'll definitely
help here. p for platinum is 10.6 x 10^-8 ohm*meters.
So, since we know of the relationship R4R1 = R2R3, this should be a breeze.
R4 = (R2R3)/R1
R4 = (46*3.48)/38 = 4.2126 ohms.
Now use R = pL/A.
4.2126 = (10.6x10^-8)L/ pi((1/2*.92 x 10^-3)^2)
(4.2126*pi((1/2*.92 x 10^-3)^2))/ 10.6x10^-8 = L
26.4m = L
Problem 8
If a charged capacitating duck C = 45F is connected to a resistance
R = 500 ohms, how much time will elapse until the voltage falls to 10 percent
of its original value?
V = V_0(e^-t/RC)
.1V = V_0(e^-t/RC)
.1 = e^-t/(45*500)
ln .1 = -t/(22500)
51808 seconds = t