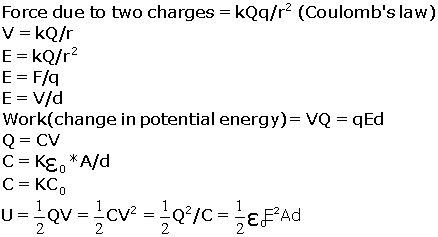
Electrostatics
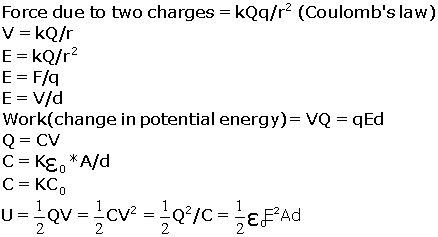
I would've spelled quack if it were possible \=<
k is the constant (approx) 9x10^9 Nm^2/C^2
it's also related to epsilon_0 (epsilon_0 is that funny looking E), permittivity
of free space.. Epsilon sub 0 = 1/4pik = 8.8542E-12 C^2/N*m^2.
E is electric field, in newtons per coulomb (N/C). V is potential difference,
in work per unit charge(a volt).
C is capicitance, which is measured in (F) farads, d is distance between charge,
which is in meters of course.
K is the dielectric constant, K*epsilon_0 = permittivity of material. (epsilon_0
is that funny looking E)
U is the energy stored in a capicator.
Q = source charge, q = test charge.
e, the charge of a proton is 1.602x10^-19C, charge of electron is -e.
1. Static charges refer to the likeliness of an object retaining
its charge. It is the loss or gain of electrons that cause an object to have
a charge. The electron theory of electrostatics states that electrons transfer
from object to object. Objects with like charges repel, objects with opposite
charge attract.
2. Conductors are materials that are likely to lose electrons,
they have a poor ability to retain static charge. Insulators on the other hand,
are materials that have the property of being able to retain charge well.
3. In order to charge an electroscope by conduction, a charged object
is brought into contact with the electroscope, transferring the electrons in
that manner. Once the charged object is removed, the electroscope will maintain
the charge of the object and indicate this by the leaves spreading. For induction,
the charged object is in proximity but not touching the electroscope, this causes
the charge to separate in the electroscope, a person can then touch the electroscope,
acting as a conductor for the electrons to pass through to the ground. Once
the object is removed from near the electroscope, the electroscope then has
the opposite charge since the like charges were repelled by the charged object
and the opposite charges were attracted by the charged object.
4. Coulomb’s law states that the force due to a charge is Fc
= kQq/r^2. k is the constant 9E9 Nm^2/C^2. Q is the source charge, q is the
test charge, r is the distance between the charges.
5. The electric field acts over a distance. It extends outward
from every charge and permeates all of space. A field is not a kind of matter.
It has force lines which are perpendicular to the equipotential lines of the
field. The direction of the force lines are from positive to negative electrode.
If the distance between a negatively charged plate and a positively charged
plate is lessened and the potential difference is held constant then the field
will be stronger, if the distance is increased then the field will be weaker.
6. The shape of the equipotential lines for these two plate
electrodes were mainly linear, except at the ends of the plate electrodes where
the equipotential lines would tether off. The force lines were linear from plate
to plate, crossing the equipotential lines perpendicularly.
Likewise for point electrodes, the magnitude of the electric field can be found
by the equation E = V2-V1/d. For point electrodes, the equipotential lines “radiated”
from the electrode; somewhat like concentric rings. The force lines were curved
from point electrode to point electrode. For both plate electrode and point
electrode, the field lines cannot cross themselves; same goes for the equipotential
lines.
7. Contrary to the statement provided, there is no electric field inside
a spherical shell conductor. On the outside though, the electric field extends
infinitely. The charge distributed on the inside of the shell is opposite to
that of the inner source charge. On the outer surface, is the like charge.
8. Force lines are the lines that of which a positive test
charge will travel upon. These lines have direction, usually from the negative
node to the positive node. Equipotential lines are perpendicular to the force
lines, they describe the path that of which an electron has equivalent electric
potential
9. Electric potential is defined as the potential energy per
unit charge. V is thus used, voltage, V = kQ/r. Also, V = PE/q. The difference
in potential is just the voltage at point a minus the voltage at point b.
10. Electric field strength can be calculated by the following equations,
E = V/d, E = F/q, and E = kQ/r^2.
11. The electron volt is a unit of energy, 1 eV = 1.602 x
10^-19J. This is an easier unit to use since it will make it a nicer number.
After you solve things in terms of J, you can convert them to eV.
12. To calculate the electric potential of a single charge,
given a distance r, you use the equation V = kQ/r. Q is the magnitude of charge,
k is the constant 9 x 10^9 and r is the distance from the single charge
13. A capacitor is a device that can store electric charge.
It consists of two conduction objects placed near each other, but not touching.
It uses the separation of charge concept.
14. Q = CV, C = epsilon nought A/d, if a dielectric is present
then multiply by K, the dielectric constant. Basically all you do is rewrite
the equations in terms of what you know and solve for C.
15. To calculate the energy stored in a capacitor, you use
the equations: U = 1/2CV^2 = 1/2Q^2/C = 1/2QV. It’s necessary to take
the givens or the possible variables that are solvable and to use the appropriate
equation
The following explains how to use an electroscope; it also identifies what
is going on and explains what is happening to the electrons.
In order to charge an electroscope by conduction, a charged object is brought
into contact with the electroscope, transferring the electrons in that manner.
Once the charged object is removed, the electroscope will maintain the charge
of the object and indicate this by the leaves spreading. For induction, the
charged object is in proximity but not touching the electroscope, this causes
the charge to separate in the electroscope, a person can then touch the electroscope,
acting as a conductor for the electrons to pass through to the ground. Once
the object is removed from near the electroscope, the electroscope then has
the opposite charge since the like charges were repelled by the charged object
and the opposite charges were attracted by the charged object.
Using the electron theory to explain how this works, in conduction the charged
object is brought into contact with the electroscope. The electrons transfer
here, if the object is charged positively, it will carry some electrons of the
electroscope away making the electroscope positive, and if the object is negatively
charged, it will repel the electrons in the electroscope and transfer some more
electrons over which are attracted to the positive charges; when the object
is brought away the electroscope will then have the charge of the charged object.
For induction on the other hand, the charged object and the electroscope never
makes contact and no electrons are transferred between the charged object and
the electroscope. What happens is the electrons move towards and away from the
charged object, depending on the charge. If the charged object is negative,
the electrons move further away in the electroscope from the object, and if
positive, they will move towards the end near the charged object. A person can
touch the electroscope when a charged object is brought near which then lets
the electrons flow away leaving the electroscope charged when the charged object
is removed.
Problem 1
Ducks of charge +70, +48, and -80 microCoulombs are placed in a line. The center
one is 0.35m from each of the others. Calculate the net force on each duck due
to the other two ducks.
Solve for the force for duck 1 to duck 2, duck 1 to duck 3, duck 2 to duck
3. Remember to change to coulombs!
D1, D2 - Plug all the info into F_charge = (kQ1Q2)/r^2. 246.857N
D1, D3 - Same as above, remember that r is 0.7m now. -102.857N
D2, D3 - Same as above, r is 0.35m. 282.1224N.
Take the sums of the forces. Draw a picture of the layout to help determine
what's going on.
For D1, -246.857N + 102.857N = -144N, to the left.
For D2, 246.857N + 282.1224N = 528.979N, to the right.
For D3, 102.857N + 282.1224N = -384.979N, to the left.
Problem 2
Three positive happy ducks of charges 11.0 microCoulombs are locatedat the corners
of an equilateral triangle of side 0.15. Calculate the magnitude and direction
of the net force on each duck.
This one requires some knowledge of vectors of course.
Solve for the forces, and draw a picture!
F_charge = (kQ1Q2)/r^2. Substitute in, determine that the force equals 48.4N.
Since this is an equilaterial triangle, add the vector components.
X: 48.4N cos 0 degrees. + 48.4 cos 60 degrees.
Y: 0N cos 0 degrees + 48.4N sin 60 degrees.
Now, apply pythagorean theorem..
83.8N away from the center.
Problem 3
A duck with a charge of +6.00mC is placed at each corner of a square
1.00 m on a side, Determmine the magnitude and direction of the force on each
duck. Note( The m in mC means x 10^-3! )
This one is also some vector stuff.. As usual, use the formula F_charge = (kQ1Q2)/r^2.
Substitute in to figure things out. Note that one of the "r" will
be sqrt(2) since it is a 45, 45, 90 triangle.
These are the vectors you SHOULD'VE come up with. (the addition sign seperates
the vector components)
X: 3.24x10^5 cos 0 + 0 +1.62 x 10^5 cos -45.
Y: 0 + 3.24x 10^5 sin 270 + 1.62 x 10^5 sin -45.
Find the vector component sums, 4.38x10^5 and -4.38x10^5.
Pythagorean theorem... 6.2x10^5 N away from the center.. Pretty easy right?
Problem 4 ( PROBLEM 3 WITH A TWIST! )
Instead of 4 positive ducks at each corner of the square, now try it with two
evil chickens with charges of -6.00mC at opposite corners of the square, along
with two positive ducks at the other pair of opposite corners with charges +6.00mC.
Apply F_charge = (kQ1Q2)/r^2, keeping note of the charge with sign.
The vectors you should come up with..
X: -3.24x10^5 cos 0 + 0 + 1.62x10^5 cos -45.
Y: 0 + -3.24x10^5 sin 270 + 1.62x10^5 sin -45.
(the addition sign seperates the vector components)
Find the vector component sums, which are -2.1x10^5 and 2.1x10^5..
Apply pythagorean theorem.
2.96985x10^5 N towards the center.
Problem 5
Compare the electric force holding a duck with the mass and charge of an electron
in orbit around a penguin that has the mass and charge of a proton in a particle
much like hydrogen's nucleus with the gravitational force between the same duck
and penguin. What is the ratio of these two forces if the distance between the
duck and penguin is 0.53x10^-10 m?
You'll need two formulas this time..
F_charge = (kQ1Q2)/r^2
F_gravity = (Gm1m2)/r^2
Plug it all in.
F_charge = ((9.9x10^9)(1.602x10^-19)(-1.602x10^-19))/(.53x10^-10)^2 = -8.2x10^-8
N
F_gravity = ((6.67x10^-11)(1.6726x10^-27)(9.11x10^-31))/(.53x10^-10)^2 = 3.618x10^-47
N
Now just divide the force of the charge and gravitational force to get the ratio
of 2.266x10^39.
Problem 6
Calculate the magnitude and direction of the electric field 2m from a single
duck with a charge of 1.6x10^-19C.
E = kQ/r^2.
E = (9x10^9*1.6x10^-19)/2^2
3.6x10^-10N/C away from the positive charge.
Problem 7
Two ducks lie in a line 1.5m apart from each other. Duck 1 has a charge
of 1.3 microCoulombs, duck two has a charge of 3.9 microCoulombs. What is the
magnitude and direction of the produced electric field midway between the two
charges?
E = k*duck1/r^2
E = 9x10^9*1.3*10^-6/.75^2
E = 2100 N/C ->
E = k*duck2/r^2
E = 9x10^9*3.9x10^-6/.75^2
E = 6200 N/C <-
4.1x10^4N/C towards duck 1.
Problem 8
What is the acceleration of a duck in a 200 N/C electric field? Mass
and charge of duck is approximately the same as that of an electron.
E = F/q
E = ma/q
2200 = 9.11x10^-31*a/1.602x10^-19
3.86x10^14m/s^2 = a
Problem 9 (OOH A TOUGHIE!)
A duck, mass m = 9.11x10^-31 kg, charge -1.602x10^-19C, is accelerated in the
uniform field E (E = 1.85x10^4N/C) between two parallel charged plates. The
distance between these two plates is 1.2cm. The electric duck is accelerated
from rest near the negative plate and passes through a tiny hole in the positive
plate. With what speed does it leave the hole?
Relate kinetic energy to electric potential energy..
E = F/q. F = Eq.
KE = /\PE.
/\PE = Work = F*d
1/2mv^2 = Eqd.
1/2 * 9.11x10^-31 * v^2 = 1.85x10^4 * .012 * 1.602x10^-19
v^2 = 7.8x10^13
v = 8836160m/s.
Problem 10
What is the magnitude and direction of the electric force on a duck with the
charge and mass of an electron in a uniform electric field of strength +3500N/C
that points due east?
E = F/q
3500 = F/1.602x10^-19.
F = 5.607E-16 N/C west, opposites attract!
Problem 11
What is the magnitude and direction of the electric field 30.0 cm directly above
a duck with a 33.0 x 10^-6 C charge?
E = kQ/r2
E = 9x10^9 *33x10^-6/.3^2
E = 3.3x10^6N/C up, the duck is the frame of ref.
Problem 12
A uniform electric field exists between two plate electrodes that are 6.0 cm
apart. 9.6 x 10^-18 J of work is needed to move one electroduck from the negative
electrode to the positive electrode. A) Was the work done by the field or an
outside source? B) What is the potential difference between the electrodes?
C) What is the strength of the electric field between the plates? D) What average
force was exerted on the electroduck by the field? E) How many electron-volts
were required to move the electron? F) What is the speed of the electroduck
as it reaches the positive electrode?
I hope you recall that an electroduck is very much like an electron.
A) Work is done by the field, the electroduck is of negative charge, which
is naturally repelled from the negative electrode to the positive electrode.
B) V = w/q. V = 9.6x10^-18J/1.602x10^-19 = 60V.
C) E = V/d 60/.06 = 1000 N/C
D) F_charge = Eq. 1000*1.602x10^-9 = 1.602x10^-16N.
E) 9.6x10^-18J x 1eV/1.602x10^-19 = 60eV.
F) 1/2mv^2 = /\PE. 1/2*9.11x10^-31*v^2 = 9.1x10^-18J. v = 2.1x10^13m/s.
Problem 13
A lightning bolt thrown by aducky transfers 30C of charge to the earth through
a potential difference of 3.5x10^7 V. How much energy is dissapated?
w = vq. w = 3.5x10^7*30 = 105x10^7 J.
Problem 14
The potential difference between two parallel wires in air is 120 V. They carry
equal and opposite charge of magnitude 95 pC. What is the capicitance of the
two wires?
Q = CV.
95pC = C120V.
C = .79pF
Problem 15
How much charge flows from a 12.0V battery when it is connected to
a 9.00-microFarad capicitor?
Q = CV
Q = 9.00microF*12.0V
Q = 108microCoulombs
Problem 16 (a toughie!)
In the ducklington model of the hydrogen atom, an electroduck orbits a protoduck
in a circular orbit of radius .53x10^-10m. A) What is the electric potential
at the electroduck's orbit due to the protoduck? b) What is the kinetic energy
of the electroduck? C) What is the total energy of the electroduck in its orbit?
D) What is the ionization energy -- The energy req to remove the electron from
the atom and take it to r = infinity?
A) E = kQ/d^2, PE = QEd => PE = kQ^2/d
PE = 9x10^9*1.602x10^-19^2/.53x10^-10 = 4.358x10^-18J
Ooops, fooled you. Electric potential is V = kQ/r. So, substitute it in and
get 27.2V.
B) First, solve the for the electric force on electron due
to proton and the gravitational force. Take the sum for net force, which is
centripetal force, equal to mv^2/r.
F Charge + F Grav = F Net
Uhh nevermind! the gravitational force is too miniscule, so just use the force
due to charge, solve using Coulomb's Law.
F Charge = kQq/r^2 => 9x10^-19 * 1.602x10^-19^2/.53x10^-10^2 = 8.22x10^-8N.
8.22x10^-8N = mv^2/r
sqrt((8.22x10^-8*(.53x10^-10))/9.11x10^-31) = 2186828m/s
Now that you've determined velocity, solve for kinetic energy with 1/2mv^2.
And it should be half the potential energy, 2.178x10^-18J.
C) Add the PE and Ke together to get 6.536x10^-18J..
D) lsmsrbls totally helped me on this
one.. kudos!! (^)<
Bond energy = PE + KE.
KE = -1/2PE (<lsmsrbls> You use F = (1/4 pi epsilonnaught) (q1q2/r^2).
K = 1/2 mv^2. F = mv^2/r. But you set the forces equal. And solve for v^2. U
= - (1/4 pi epsilonnaught)(q1q2/r). [err. . .. refer to part B hehe]
Bond Energy = 1/2PE.
1/2(4.358x10^-18J) = 2.178x10^-18J.
Bond energy is - so 2.178x10^-18J is required.
Problem 17
550V is applied to a 7200pF capacitor. How much energy is stored?
U = 1/2CV^2. U = 1/2*7200pF*550V = 1.09x10^-3J
Problem 18
A homemade capacitor is assembled by placing two 9 inch pie pans with
duck emblem10cm apart and connecting them to the opposite terminals of a 9V
battery. a) estimate the capacitance, b) the charge on each plate, c) the electric
field halfway between the plates, d) the work done by the battery to charge
the plates. e) Which of the above values change if a dielectric is inserted?
a) A = .164m^2. Ke_0A/d = C = 1.0006*8.81x10^-12*.164/.1. C = 3.6pF
b) The charge on each plate can be found by Q = CV. 3.6pF * 9.0V = 32pC
c) The electric field halfway between the plates can be found by V/d = 9/.01
= 90V/m
d) The work done by the battery to charge the plates is w = vq = Ed = 1.5x10^-12J
e) Capacitance, charge, and work done by battery.
Problem 19
How much energy is stored by the electric field between 2 plates 7.0cm x 11.0cm
seperated by a 3.0mm air gap, when the charge on the plates is 300microCoulombs?
Ke_0A/d =C
(1.006*.8.85x10^-12*.07*.11)/(3/1000) = C
2.2786x10^-17 = C
U = 1/2Q^2/C = U = 1/2*300x10^-6^2/2.2786x10^-17 = 1980J
Problem 20
How does the energy stored in a capacitor change if a) the potential
difference is doubled, b) the charge on each plate is doubled, and c) the seperation
of the plates is doubled, as the capacitor remains connected to a battery?
a) Since the capacitor remains connected to the battery, the C stays the same.
checking out the equation U = 1/2CV^2, you can see that the energy stored will
increase by 4x.
b) Since the charge on each plate is doubled, and there is the equation U =
1/2QV, you can see that it will also increase by a factor of 4, since there
are two plates, and 2*2 = 4.
c) If the distance between the plates is doubled, C = e_0A/d then it will be
1/2 the energy stored.
Problem 21
There are four charges, each with a magnitude of 1.6 µC. Two are positive and two are negative. The charges are fixed to the corners of a 0.33 m square, one to a corner, in such a way that the net force on any charge is directed toward the center of the square. Find the magnitude of the net electrostatic force experienced by any charge.
By intuition, the situation seems to imply that the charges are laid about the square so that they alternate sign.
After figuring this out, we can now use Coulomb's law, F = kQq/r^2.
Choosing an arbitrary charge, the "bottom left" one for instance, we can first find the force vectors on the two adjacent charges.
F1 = kQq/r^2, F = (kq^2/r^2)i (it is being attracted by the oppositely charged charge in the i direction)
F2 = (kq^2/r^2)j (it is being attracted by the oppositely charged charge in the j direction).
Now for the charge on the opposite corner of the square, we have an r of Sqrt[r^2+r^2]
F3 = -kq^2/(2r^2)*cos(pi/4)i + -kq^2/(2r^2)*sin(pi/4)j (it is being repelled by the like charged charge away from the center.
Summing up all the forces, we get ((4-Sqrt[2])kq^2/4r^2)i + ((4-Sqrt[2])kq^2/4r^2)j. This makes sense since it is a symmetric situation.
Making substitutions, we have a net force of 0.137Ni + 0.137Nj => 0.193N towards the center.
Problem 22 thanks ]JJD[
There is an electric field near the Earth's surface whose intensity is about 150 V/m. How much energy is stored per cubic meter in this field?
Basically, you're looking for the energy density of the given electric field.
If you treat the earth "like a capacitor," the energy is given by U = 1/2CV^2.
Making the substitutions of C = K*eps_0A/d (we assume K = 1 here) and V = Ed, U then equals 1/2*eps_0*A/d*E^2*d^2.
U = 1/2*eps_0*A*E^2d, Ad = volume, so energy density = 1/2*eps_0*E^2.
Substituting E = 150, we get 9.95*10^(-8)J/m^3
Problem 23
A uniform electric field has a magnitude of 2.4*10^3 N/C. In a vacuum, a proton begins with a speed of 2.4*10^4 m/s and moves in the direction of this field. Find the speed of the proton after it has moved a distance of 3.0 mm.
So we have an initial velocity for a proton, and it is being accelerated by the electric field.
Using the work-energy theorem, Work = qEd = dKE
KE = 1/2mv^2, so. qEd = 1/2m(v^2-v0^2)
Sqrt[2qEd/m+v0^2] = v. Substituting everything in, we get 44242m/s