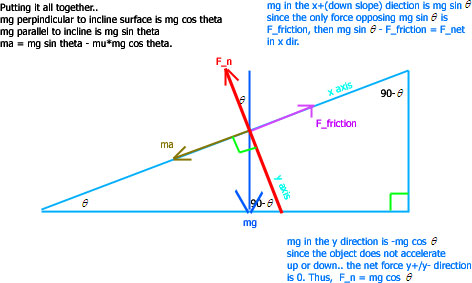
Variation is ma = -mg sin theta - mu*mg cos theta if motion of block is UP slope.
Inclined Plane Motion

Variation is ma = -mg sin theta - mu*mg cos theta if motion of block is UP slope.
Problem 1: Several ducks have been toying with the idea of pushing a chicken into an oven. Sadly, their attempt to push the fat chicken horizontally across a level ground into the oven proved futile since the oven was a couple meters off the ground. One duck came up with the bright idea of setting an inclined plane next to the oven, so that they could simply push the chicken along the slope. The inclined plane is of length 5 meters, with an angle of 25 degrees. If the team of ducks give the chicken an initial velocity of 4.0m/s from the bottom of the plane. Will the chicken make it into the oven? If not, how far up the inclined plane will it go? The coefficient of friction between the chicken and the plane is 0.30.
To determine if the chicken will make the oven, we must first find the acceleration.
Let going down the plane be the +x. a = - g sin theta - mu g cos theta. (g sin
theta is negative because it is going up the plane)
a = -9.8 sin 25- 0.3(9.8) cos 25.
a = -6.8m/s^2
Then we use the kinematic equation, v^2 = v0^2 + 2a(x-x0).
0 = 4^2 + 2(-6.8)(x)
1.176m = x
Thus, no the ducks were not able to push the chicken into the oven. To
determine how much initial velocity the ducks must've given the chicken, we
can use
v^2 = v0^2 + 2a(x-x0) once again.
0 = v0^2 +2(-6.8)(5).
8.246m/s = necessary initial velocity
Problem 2: a 40.0-kg wagon is towed up a hill inclined at 18.5 degrees with respect to the horizontal. The tow rope is parallel to the incline and has a tension of 140N in it. Assume that the wagon starts from rest at the bottom of the hill, and neglect friction. How fast is the wagon going after movign 80.0 m up the hill?
Write the equation for net force parallel to the incline.
F_net = F_tension - W_parallel
F_net = 140 - mgsin(18.5)
F_net = 15.6392
a = 0.39098m/s^2
Now, back to kinematics.
v^2 = v0^2 + 2ad.
v^2 = 2*0.39098*80
v = 7.90929m/s
Problem 3: A block of mass m = 2.00 kg is released from rest h = 0.500 m from the surface of a table, at the top of a theta = 30.0° incline. The frictionless incline is fixed on a table of height H = 2.00 m. (a) Determine the acceleration of the block as it slides down the incline. (b) What is the velocity of the block as it leaves the incline? (c) How far from the table will the block hit the floor? (d) How much time has elapsed between when the block is released and when it hits the floor? (e) Does the mass of the block affect any of the above calculations?
a) Using the free body diagram, we can determine the equation for net force to be mgsin(theta). solving for a, 4.9m/s^2.
b) The block slides a distance of 1 m along the incline (0.5/sin(30)), now we can use v^2 = v0^2 + 2ad. v = 3.13m/s.
c) Since we found the resultant velocity, we want the horizontal component now so we can use d = v_x*t in the horizontal. 3.13cos(30) = v_x, t is given by y-y0 = v_yt + 1/2gt^2, v_y is 3.13sin(30), and by using the quadratic equation we arrive at t = 0.499s. d is then 1.35m.
d) The time for part b is given by y-y0 = 1/2gt^2, Sqrt[2*2/g], t = 0.639s. The total time is then 0.639 + 0.499 = 1.14s.
e) The mass of the block doesn't affect the calculations since air resistance is ignored. In part a, the mass cancels out in the net force equation.
Problem 4: A mass m1 on a frictionless plane inclined at X degrees with respect to the horizontal is connected via a massless rope to a massive pulley of moment inertia I. At the other end is a hanging mass m2. Find the expression for the net acceleration of the system. (thanks orakle)
Choosing to assume that the system will rotate such that the mass m1 slides down the incline..
The torque on the massive pulley is
(T1-T2)R = I*alpha.
The tension in the part of the rope that connects to m2 is pulling upwards then, so T2 - m2g = m2*a.
The mass m1 is being pulled back in the other direction by the tension, m1g*sinX - T1 = m1*a. It is sinX because that is the component of weight parallel to the incline.
Solving the system..
-T2 + m2g = -m2*a
-m1g*sinX + T1 = -m1*a
T1 - T2 + m2g - m1g*sinX = -m2*a - m1*a
T1 - T2 = -m1*a - m2*a - m2*g + m1g*sinX
Make the substitution into the equation for torque.
a = R*alpha
T1 - T2 = Ia/R^2
Substitute T1 - T2 found above in.
-m1*a - m2*a - m2*g + m1g*sinX = Ia/R^2
Solve for a
-m1*a - m2*a - Ia/R^2 = m2g - m1g*sinX
-a(m1+m2+Ia/R^2) = m2g - m1g*sinX
a = (m1g*sinX - m2g)/(m1+m2+Ia/R^2)