Physics

Geometric Optics
So..

	Law of reflection, the angle of incidence equals the angle of reflection.
	The focal length is half the radius of curvature.
	This is called the mirror equation. f denotes the focal length, d_o is the object distance, d_i is the image distance. Make sure you realize that these values can be negative as they are displacement from the mirror.
	m is the lateral magnification of the mirror. h_i is the height of the image, h_o is the height of the object. d_i is the image distance, d_o is the object distance.
	n, the index of refraction of a material is equal to the speed of light in a vacuum (approximately 3.00x10^8m/s) over the speed of light in the respective material.
	This equation is known as Snell's Law. The left side of the equation with subscript 1 corresponds to one medium and its angle of incidence. The right side with subscript 2 corresponds to another medium and the angle of refraction.
	Theta_c, is the critical angle. This is the incident angle that of which the angle of refraction will be 90 and the refracted ray will skim the surface of a material.

For a plane mirror, light is reflected at the same angle that of which it strikes the mirror. The ray of light that strikes the mirror is referred to as the incident ray. The ray of mirror that reflects off the mirror is called the reflected ray. The angle of incidence and the angle of reflection, named respectively, are equivalent when taken from the normal. The normal is the line that bisects the full angle such that the angle of incidence and angle of reflection are equivalent. This normal is perpendicular to the plane mirror as well. The virtual image in a plane mirror is skewed proportionally to the actual image. The size of the virtual image depends on the distance between the actual image and the plane mirror. The further away the actual image is from the plane mirror, the smaller the virtual image appears. The closer the actual image is from the plane mirror, the more similar in size the virtual image is to that of the actual image. To apply the law of reflection to surfaces that are not flat, treat the point that the incident ray strikes as a plane mirror. From here, draw the tangent to that point and the plane mirror. The reflected ray can be obtained because of the law of reflection that states the angle of incidence is equivalent to the angle of reflection.

For a concave mirror, when the object is located beyond the center of curvature, there will be a real image which is smaller, inverted and it will appear in front of the mirror. When the object is located at the center of curvature, there will be a real image, inverted, same size as object, located at the center of curvature which is in front of the mirror. When the object is located between the center of curvature and the focal point, there will be a real image, which is inverted and larger, in front of the mirror. When the object is located at the focal point, there will be no image because the reflected rays are parallel. When the object is located between the focal point and the mirror, there will be a virtual image which is erect, beyond the mirror, and larger.

For a convex mirror, the images formed will always be virtual, erect, smaller, and beyond the mirror.

Refraction is the bending of light. When a ray of light is incident on an interface between two different mediums, a generalization can be made. If the index of refraction of the medium the incident ray travels through is greater than the index of refraction of the medium the emergent ray travels through, then the angle made by the incident ray to the normal will be less than the angle made by the emergent ray to the normal. If the index of the medium through which the incident ray travels through is less than that of the medium of which the emergent ray travels through, then it is just the opposite. Light tends to bend towards the normal when it passes from a material of lower index of refraction to that of a higher index. It tends to bend away from the normal as it passes from material of higher index to lower index. The index of refraction is a constant for a given material, which is the ratio c/v, where c is the speed of light in a vacuum and v is the velocity of light in that respective material.

A Summary.

1. The ray model of light suggests that light travels in straight lines under a variety of circumstances. Geometric optics is the study of straight line rays at various angles.

2. The law of reflection states that the angle of incidence equals the angle of reflection. On a flat surface, the normal perpendicular to the surface is that of which the angle of incidence and reflection are measured from.

3. The image formed by a plane mirror is thus follows: virtual, inverted, same size, beyond, and equidistant from the plane mirror.

4. The three rules for locating an image formed by a mirror are as follows.. If the mirror is concave, draw a parallel line from the top of d_o to the axis, then reflect through f. Next from top of d_o go through f to axis then reflect parallel. Next, from top of d_o through the origin of axis. These will meet at a single point where you can draw the image formed perpendicular to the axis.

5. Real images are formed by converged light rays. Virtual images are formed where light doesn’t actually reach. The rays reflect back into the eye.

6. For a concave mirror, if the object is beyond C, the image will be in front of C, inverted, real, and smaller. For at C, it will be the same size, inverted, real and in front of the mirror. Between C and F, the image is inverted, larger, and real. At f, there is no image. Between F and the mirror, the image will be beyond the mirror, virtual, larger, and erect. For a convex mirror, the image will be erect, virtual, smaller, and located beyond the mirror.

7. The relationship between the focal length and the radius of curvature is that f = R/2.

8 . Refraction is the bending of light, due to the change in velocity of light in a specific medium. The index of refraction of a medium is the speed of light in a vacuum over the velocity of light in a given medium.

9 . Total internal reflection occurs when the angle of refraction is 90. This can only occur if the second medium of the interface has a lesser index of refraction.

10 . Converging lenses take light parallel to the optical axis and “converge” it upon the focal point. Diverging lenses diverge light parallel to the optical axis such that when the rays are extended they meet at the focal point.

11. The rules for making a ray diagram for lenses are as follow. From the top of d_o, draw a parallel to the optical axis then have it go through f’. Next, from the top again, draw it through f, then extend it to axis, then draw parallel to optical axis. Finally, draw from top of d_o through origin of axis. These three should meet at the same point, where you can then draw d_i.

12. To solve a problem with combination lenses, pick a starting lens, find the image, use the image as the object for the second lens, and repeat.

Problem 1
An object stands 30 cm in front of a thin converging lens with a focal length of 15 cm. Describe the image formed.

Since the lens is converging, f is positive. Use the lens equation, f^-1 = d_0^-1 + d_i^-1 to find that d_i is +30cm. m = -d_i/d_o, so m = -1.
Since d_i is +, the image is 30cm -behind- the lens and -real-.
Since m is -, the image is inverted.
Since m is 1, they're the same size.

A little about the eye..

1. The eye focuses on objects at different distances by the process of accommodation. To focus on a nearby object, the muscles contract, causing the center of the lens to be thicker, which then shortens the focal length. For a far away object, the muscle relaxes so that the lens is thinner. This increases the focal length.

2. A nearsighted eye has the problem that the eyeball is too long, or sometimes the curvature of the cornea is too great. The objects are focused in front of the retina then. This can be corrected with a diverging lens, since it causes the light to diverge then be refocused at the retina. A far sighted eye is just the opposite. The eyeball is too short, or the curvature of the cornea isn’t curved enough. This can be corrected with a converging lens.

Problem 1
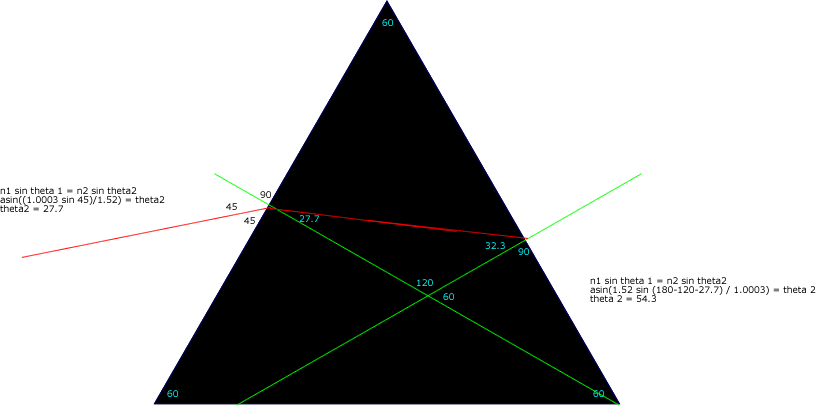
A ray of monochromatic light enters an equilateral triangle made of crown glass ( n = 1.52 ) at 45 degrees to the normal, at what angle does it exit the triangle?

The Wave Nature of Light

2t=(2m+1)*lambda/2n	minimum thickness of soap bubble skin formula. m is the order, n is the index of refraction.
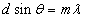	m is the order of the fringe, lambda is the wavelength of the light beam, d is the distance between two slits.

1. The interference of waves depends on the amplitudes, phase of the waves and wavelength. There will be constructive interference when the paths of the two waves differ by one wavelength, or any whole number of wavelengths. Destructive interference occurs when the wavelengths differ by a half. Diffraction is affected by slit width and wavelength. Larger the slit, the more bands there will be. Longer the wavelength, the more bands there will be.

2. Evidence that shows light has wave properties are that light waves interfere with each other constructively and destructively, as well as show diffraction patterns.

3. The longest wavelength of visible light is 750nm, which is the color red. The shortest the wavelength of visible light is 400nm, which is the color blue.

4. Dispersion is the spreading of white light into a full spectrum. This can be observed when white light is incident on a prism, or white light shining through a diffraction grating. After passing through either the prism or the diffraction grating, a spectrum of colors can be seen.

5. The equations you want to know for solving problems involving interference due to reflection and diffraction are: sin theta = lambda/D, m*lambda = d sin theta, where m is the order. Tan theta = distance from central/screen distance.

6. When white light is passed through a prism, the index of refraction depends on wavelength, so the different wavelengths(colors) are bent to varying degrees. Violet light is bent the most since index of refraction is greater for shorter wavelengths. Red is bent the least. When light passes through a diffraction grating, the light diffracts at every opening between the parallel lines of the grating. Since it diffracts the light so much into its component wavelengths, the pattern ends up being a spectrum

7. Line spectrum are characteristic of gaseous compounds at normal temperature. This occurs when the gas is heated or a large electric current is applied to the compound. Light from heated solids such as a lightbulb’s filament and even gases under high pressure produce a continuous spectrum. Absorption lines also occur since atoms and molecules can absorb light at the same lambdas that they emit light at.

8. Colors are formed by interference of thin films because the incident light reflects both from the top layer and the bottom layer of the thin film. When this occurs, interference can occur, which produces the color.

9. The effect of polarizing light is that the light is confined to a plane of travel. Polaroids can be used as sunglasses, optical stress analyzers, or even a method to enrich photography. It’s also used in kaleidoscopes.

We'll start off with an appetizer.

Problem 1
Monochromatic light falls on two very narrow slits 0.040mm apart. Successive fringes on a screen 5.00 m away are 5.5cm apart near the center of the pattern. What is the wavelength and frequency of the light?

This is a rather tricky question, but once you understand it, it makes all the following problems easier.
Well, start off by drawing a picture, one of the best methods of problem solving (in my opinion). Since we know d = 0.040 x 10^-3 m, and the distance between the slits and the screen is 5.00m, then drawing a triangle reveals theta to equal the arctangent of (5.5x10^-2)/5. Now that we have theta, substituting things in is easy.
You should come up with lambda equaling 440 nanometersif you let m, the order, equal 1.

Finding the frequency can be achieved by c = lambda*nu, where nu is the frequency and c is the speed of light in a vacuum.
nu = c/lambda.
3.0*10^8/(440*10^-9) => 6.82 x 10^14 Hz.

Problem 2
A parallel beam of light from an angry duck with a wavelength of 656 nm falls on two very very narrow slits, 0.050 mm apart. How far apart are the fringes in the center of the pattern if the scren is 2.6 m away?

Using the triangle again, the arctangent of 656*10^-9/(0.050*10^-3) results in theta. Now we can use the triangle with screen distance and inteference fringe length once again.
tan theta = x/2.6 ( x is the interference fringe length.)
3.4*10^-2 m = d.

Problem 3
Light of wavelength 680 nm falls on two narrow slits and produces an interference pattern of chickens in which the fourth-order fringe is 48 mm from the central fringe on a screen 1.5 m away. What is the seperation of the slits?

Here, we want to find "d."
Using the triangle.. (hey look lots of triangles) theta = arctangent(48*10^-3/1.5)
Now that we have theta.. substitute into m*lambda = d sin theta.
(4*680*10^-9)/Sin[ArcTan[(48*10^-3)/(1.5)]] = d
8.5*10^-5 m = d.

Problem 4
Light of wavelength 400 nm in air falls on two slits 5.00 * 10^-2 mm apart. The slits are immerse in chicken blood (index of refraction 1.33), as is a viewing screen 40.0 cm away. How far apart are the fringes on the screen?

Mmmm (^)< QUACK QUACK QUACK chicken blood.
Anyway.. We solve for theta not using the triangle starting off.
m*lambda = d sin theta.
400*10^-9/(5*10^-5) = sin theta.
Now that we have theta, we know that there is refraction.. so use Snell's law. n1 sin theta 1 = n2 sin theta 2.
Now we have theta 2 which is approx .3446.. and Hey it's another triangle with the viewing screen.
tan theta2 = x/(40*10^-2). (where x is the distance between the fringes)
x = 2.406*10^-3 m for the distance from fringe to fringe.

Problem 5
EM waves from a line source pass through a narrow slit and form an interference pattern on a screen. As the slit narrows, what happens to the width of the central maximum?
Since m*lambda = d sin theta, you notice that d is inversely proportional to the sin of theta. Therefor, as d decreases, the width of the central maximum will increase.

Problem 6
A grating has 7000 lines/cm. How many spectral orders can be seen when it is illuminated by white light?

m*lambda = d sin theta.
d = (700000 lines/cm )^-1 = 0.0001428571429 cm/line * 1 m/100cm
d = 1.428571429 x 10^-7
m = ( 1.428571429 x 10^-7 sin 90 )/(700x10^-9m)
m = .2040816327
m = ( 1.428571429 x 10^-7 sin 90 )/(400x10^-9m)
m = .3571428572