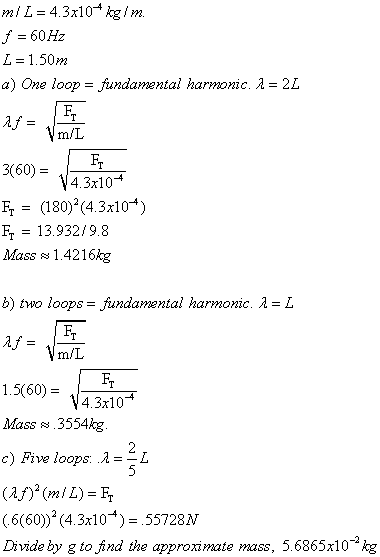
Vibration and Waves

T = 2pi*sqrt(m/k)
v = lambda*f
p = A sin(kx-wt) w=2*pi*f (pressure in travelling sound wave), k = 2pi/lambda, A = amplitude, x = displacement.

1. Periodic motion: used to describe a vibration or an oscillation that repeats itself over the same path.. Displacement: The position of an object. Amplitude: The maximum displacement. Period: The time in seconds required for one complete cycle. Frequency: The number of cycles, per second. Simple Harmonic Motion: Sinusoidal motion of a single frequency.

2. Total E = 1/2kA^2. = 1/2kx^2+1/2mv^2. EPE = 1/2kx^2.

3. The equation for the period of a spring is T = 2pi*sqrt(m/k). For example, how long does it take for a spring with a hanging mass of 5 kg and spring constant 10N/m to exhibit one complete cycle? T = 2pi*sqrt(5/10). T = 2pi*sqrt(1/2).

4. Since a period is the time it takes for one complete cycle in seconds, frequency is the inverse of the period. f = 1/T. T = 1/f.

5. For describing the motion generated SHM, you can use x = A sin 2pi*f*t. This is if the motion starts at equilibrium point. If it starts at the crest/trough of its motion, then use x = A cos 2pi*f*t.

6. For describing the motion generated SHM, you can use x = A sin 2pi*f*t. This is if the motion starts at equilibrium point. If it starts at the crest/trough of its motion, then use x = A cos 2pi*f*t.

7. The maximum velocity of a particle on SHM can be found by v = 2pi*A*f. Now, for any other velocity at a point in time, it can be found by v = v0(sqrt(1-x^2/A^2)).

8. The equation for the period of a pendulum is T = 2*pi*sqrt(L/g). L = length of the pendulum. This only works if its amplitude is small and friction can be ignored.

9. Dampened harmonic motion is the gradual decrease of maximum displacement. This is caused by the presence of frictional forces. The energy is eventually all transformed to heat.

10. Forced vibration is due to an external source, which applies its own frequency to the spring. The natural frequency of the spring is actually 1/2pi * sqrt(k/m), which is what it will actually vibrate at without external force.

11. Amplitude denotes the distance between the equilibrium and the crest or trough of the wave. Wavelength is the distance from one point of the wave to the corresponding point in the next cycle. (crest-crest). This can be found be lambda = v/f. Wave velocity is the velocity at which wave crests move. V = lambda*f. Node is referring to the point of destructive interference. Antinode is referring to the point of constructive interference.

12. The relationship between velocity, wavelength, and frequency is v = lambda*f, where lambda is the wavelength and f is the frequency, v is the wave velocity.

13. A transverse wave refers to a wave that causes the particles of the medium it travels in to move a direction perpendicular to the motion of the wave itself. On the other hand, in a longitudinal wave, the vibration of the particles of the medium is along the same direction as the motion of the wave.

14. The velocity of a longitudinal wave can be calculated by v = sqrt(elastic force factor/inertia factor). For a long solid rod, v = sqrt(E/p), where E is the elastic modulus, and p is the density. For a liquid or gas, v = sqrt(B/p) where B is the bulk modulus, and p is the density.

15. Reflection is when a wave strikes an obstacle, or comes to the end of a medium it is traveling in. A part of the wave is reflected back. Superposition is referring to the algebraic sum of waves interfering with each other. Standing waves are created when the medium is vibrating at the correct frequency. This frequency is obtained when clear nodes are formed where there is no motion, the points of destructive interference, and antinodes, the points of constructive interference. Harmonics are the frequencies where standing waves are formed. The fundamental frequency can be found by the equation v/2L or v/lambda.

16. To solve problems involving standing waves in strings, you usually find out the fundamental frequency first of all. From this you can determine a number of things, such as wavelength, wave velocity, etc.

Problem 1
One end of a horizontal string of linear density 4.3 x 10^-4 kg/m is attached to a small-amplitude mechanical 60-Hz vibrator. The string passes over a pulley, a distance L = 1.50m away, and a duck is hung from this end. What must the mass of the duck be, that is hung from the end of the string to produce (a) one loop, (b) two loops, and (c) five loops of a standing wave? Assume the string at the vibrator is a node, which is nearly true. Why can the amplitude of the standing wave be much greater than the vibrator amplitude?

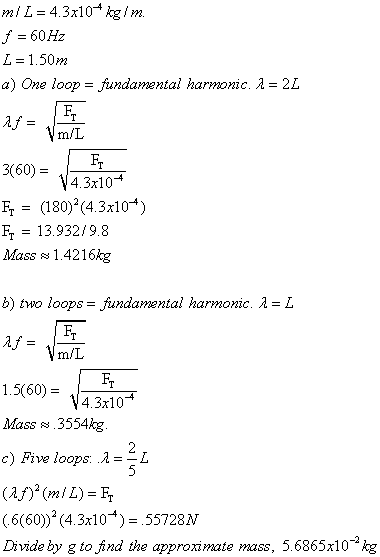The amplitude of the standing wave can be much greater than the vibrator's amplitude since the reflcting wave is from the mass.