|
problem 1 |
||
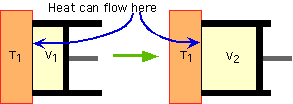
Given: p0 A sealed room, x meters on each side, filled with N2 (whose molecular weight = 28g/mol) Find: Heat required to raise the temp from T1ºC to T2ºC of N2 Solution: Use pV=NkT to find N, using p0 as the pressure, T1 as the temperature, and x^3 as the volume. Substitute that N value into the formula U = (alpha)Nk(deltaT) to get the answer. |
A
|
|
|
|
B |
|
|
|
C |
|
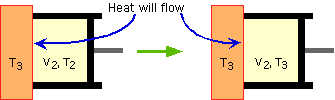
problem 2 |
|
|
|
Given: |
A
|
|
|
|
B |
|
|
Thus that equation basically becomes Q = Wby. This is what you found in part B. |
C |
|
problem 3 |
|
|
Given: X mols of nitrogen at a temp T1 in a volume Vi that is later compressed to Vf Find: Initial and Final Pressure Solution: To get the initial pressure, use PV = nRT. To get the final pressure, use P1V1^(gamma) =P2V2^(gamma) where gamma = (alpha + 1)/alpha. Alpha in this case is 5/2 because nitrogen is diatomic, meaning it has 5 degreees of freedom (it can move in the directions of the x/y/z axes, and can spin in two ways), each degree being associated with .5kT. |
A
|
|
|
|
B |
|
Given: Same Find: Work done on the nitrogen (in Joules) Solution: Won = -Wby = -(alpha)nR(T1-T2) If you haven't figured it out already, you better know which formulas on the equation sheet apply to which kind of process. |
C |
|
problem 4 |
|
||
|
|
|||
|
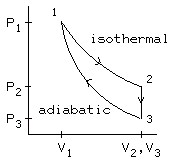
p1 Know this picture. Understand it. And not just some half assed "I know what the picture looks like," you need to understand ALL of it: how to solve for values given values in other stages, which processes are reversible, how much work is done by each stage (by the way, you don't necessarily have to calculate values for that, you can look at the picture). And that's just to name a few things. We can almost guarantee that this kind of problem will come back and bite you in the ass on an exam. |
 |
||
|
Here's what's happening:
During the constant volume (isochoric) process, the gas is cooled from T2 to T3 by putting it in contact with a reservoir at temperature T3 . (This is an irreversible process.)
During the adiabatic process, the gas is compressed while isolated from outside heat sources, so no heat flows. Work is done on the gas to compress it. The temperature rises from T3 to T1 , so the gas has returned to its original state. To find the pressure at stage 3, use the fact 1 -> 3 is an adiabatic process, so use P1V1^(gamma) =P3V3^(gamma) where gamma = 5/3, because it's a monatomic gas. |
A
|
||
|
In the following questions: Heat flow into the system,work done by the system, an increase in the internal energy of the system should be reported as positive . Heat flow out of the system, work done on the system, a decrease in the internal energy of the system should be reported as negative . Find: Work done by this system and the heat flow into the system in the transition from state 1 to state 2 |
B |
||
|
Thus, delta U = Q - Wby becomes deltaU = Q. |
C |
||
Given: Same Find: Work done by this system and the change in the internal energy of this system in the transition from state 3 to state 1 Solution: 3 -> 1 is an adiabatic, so there's no change in Q. The equation deltaU = Q - Wby can then be simplified to deltaU = -Wby. deltaU = (alpha)nR(deltaT) = (alpha)(P3V3 - P1V1). You'll probably get a positive number for the deltaU, so just make it positive to get the Wby. |
D |
||